This is part of the group project I did in course STAT447. This part of the material is not covered in lectures and totally done by myself. I believe it is a nice experience for exploring things by myself so I post the detailed version here on my personal blog.
The dataset we used is from a Kaggle competition Link here. In our group project, we tried several models: Ordinary least square (OLS), weighted least square (WLS), regression tree, quantile random forest, and time series. It turns out that the time series model is the best. The Time series model, as for what I believe, should work well in basically two cases: one is the process in nature has periodic behavior (i.e precipitation) or, for those have previous stage dependency like financial data. People always look at the previous performance when making decisions.
The dataset has very high usability with only 2.3% missing values. It contains 14 categorical variables and 48 numerical variables. The variable set consists of two parts: The true variables and the generated variables. True variables are

and those generated variables are simply the variables above at different time. One interest variable is the trade_type which is a binary variable indicating deal is made by individuals or dealers. We should expect the performance of individuals to be worse than dealers and they buy at high and sell at low more often.
Plot the series we see
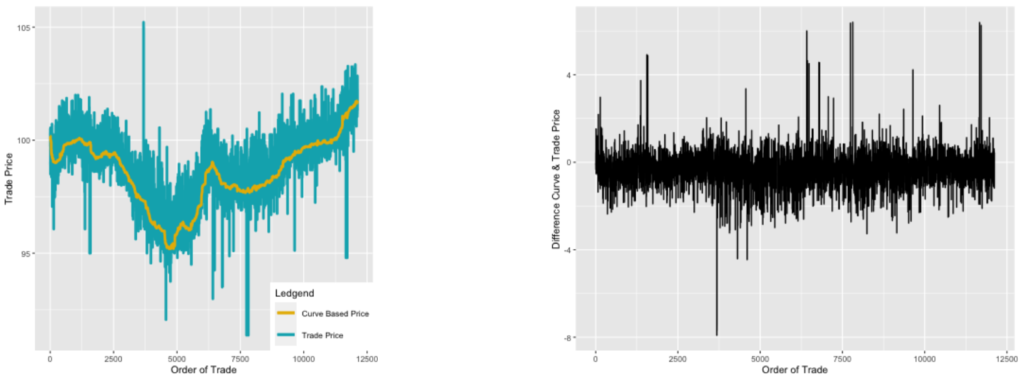
where the curve base price is computed based on the theoretical discounting formula
where F is the book value (fixed amount) then times r, the coupon rate, is the fixed coupon payment, i is the interest rate, C is the final payment. The above plot indicates two things: first, the series is not stationary with an obvious trend (i.e not mean stationary); second, the right graph shows extremely heteroscedastic. This implies two things: It is not valid to apply the usual ARMA model to the original price data (i.e stationarity required). Second, there must be a way to deal with heteroscedastic.
So the first idea to deal with non-stationarity is to do differencing which is ARIMA. The fact is that it takes me almost 20 differencing to see stationarity so this idea is abandoned. Also the ACF plots mostly shows that
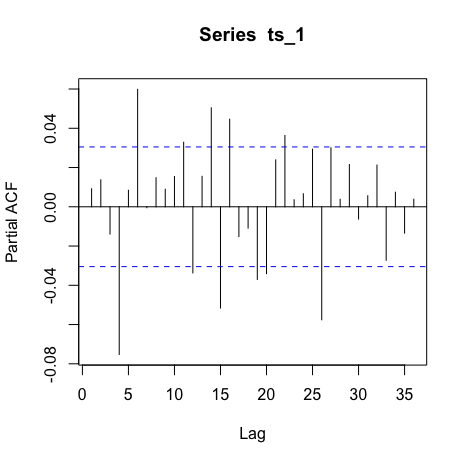
which does not give any useful information for parameter determination.
Next, I turned to do deal with the heteroscedastic. The difference between curve-based price and the actual trading price seems stationary (the right graph). Then the model suggested by TA in this course is the ARMA-GARCH model.
One important thing is that, people at time t only have access to data up to t-1 so the response variable should be
P_{t-1} - P_{\text{curve}, t}
The ARMA(p_1,q_1)-GARCH(p_2,q_2) model is in form of
Y_t = \alpha_i Y_{t-i} + \sum_{j=1}^{q_2} \beta_j e_{t-j} + e_t, e_n \sim N(0,\sigma^2)
and the grach part is
This GRACH part can handle the heteroscedastic since it regresses not only on those previous residuals but also their corresponding variance.
Now the only problem is to chose the best hyperparameter which are p_1,q_1,p_2,q_2. The time series model is different from the OLS WLS model. Its testing and training set can not be obtained by randomly drawn since it is time-dependent. You can’t fit time series without a time index. So I restructure the data to make time series for each bond then take the first 60% of time recording as a training set and the later 40% as a test set. Also, I add one more restriction
This type of constrains comes from the thought about overfitting and also since in the test set only 10 previous data is available which means we can at most have 10 parameters to predict. Notice we also need to predict \sigma^2 so in order to have a reasonable prediction, for each parameter we give 1 and then add 1 more degree of freedom for each process. I also think about adding external regressors so the code is done in two parts as follows. A prediction for a single bond should be like

where the yellow chunk is the confidence interval. Notice the following algorithm, the forecasting method is a one-step-ahead fitting. To be more specific, this is a rolling forecast one step ahead.
Model Comparsion Criterion
In the whole project, we computed different criteria including average length of the confidence interval, with alpha = 0.5 and 0.8, coverage rate, interval score with alpha = 0.5 and 0.8. I will introduce these in more detail if I got time. After obtaining the model, use the corresponding historical data to predict one step forward and then based on the predicted value to do the next prediction until the desired number of predictions (steps ahead) are obtained.
Coding up the model using package rugarch
The package I adapted in R is the rugarch. The code is divided into two parts, one is for ARMA-GARCH only and try all different combinations of p and q under a total of 6 constraints. The other one is to try adding external regressor which is decided to be tried are trade_size, trade_type, time_to_maturity, reporting_delay.
Combinations of hyper parameter candidates
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
pq_combination = list( c(0,0,1,0),c(0,0,1,1),c(0,0,1,2),c(0,0,1,3),c(0,0,1,4),c(0,0,1,5), c(0,0,2,0),c(0,0,2,1),c(0,0,2,2),c(0,0,2,3),c(0,0,2,4),c(0,0,3,0), c(0,0,3,1),c(0,0,3,2),c(0,0,3,3),c(0,0,4,0),c(0,0,4,1),c(0,0,4,2), c(0,0,5,1),c(0,0,5,0),c(0,0,6,0), c(1,0,1,0),c(1,0,1,1),c(1,0,1,2),c(1,0,1,3),c(1,0,1,4), c(1,0,2,0),c(1,0,2,1),c(1,0,2,2),c(1,0,2,3),c(1,0,3,0), c(1,0,3,1),c(1,0,3,2),c(1,0,4,0),c(1,0,4,1), c(1,0,5,0), c(2,0,1,0),c(2,0,1,1),c(2,0,1,2),c(2,0,1,3), c(2,0,2,0),c(2,0,2,1),c(2,0,2,2),c(2,0,3,0), c(2,0,4,0), c(3,0,1,0),c(3,0,1,1),c(3,0,1,2), c(3,0,2,0),c(3,0,2,1),c(3,0,3,0), c(4,0,1,0),c(4,0,1,1), c(4,0,2,0), c(5,0,1,0), c(1,1,1,0),c(1,1,1,1),c(1,1,1,2),c(1,1,1,3), c(1,1,2,0),c(1,1,2,1),c(1,1,2,2),c(1,1,3,0), c(1,1,4,0), c(2,1,1,0),c(2,1,1,1),c(2,1,1,2), c(2,1,2,0),c(2,1,2,1),c(2,1,3,0), c(3,1,1,0),c(3,1,1,1), c(3,1,2,0), c(4,1,1,0), c(1,2,1,0),c(1,2,1,1), c(1,2,2,0),c(1,2,2,1),c(1,2,3,0), c(2,2,1,0),c(2,2,1,1), c(2,2,2,0), c(3,2,1,0), c(1,3,1,0),c(1,3,1,1), c(1,3,2,0),c(2,3,1,0), c(1,4,1,0) ) |
The function for criteria
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
#Weighted Mean Squre Error WMSE_res <- function(res,w){ sum(w*abs(res))/sum(w) } #Mean Square Error MSE_res <- function(res){ sqrt(sum(abs(res)^2)/(length(res)-1)) } #Interval scores and Average length intervalScorePlus=function(predObj,actual,alpha){ n=nrow(predObj) ilow=(actual<predObj[,2]) # underestimation ihigh=(actual>predObj[,3]) # overestimation sumlength=sum(predObj[,3]-predObj[,2]) # sum of lengths of prediction intervals sumlow=sum(predObj[ilow,2]-actual[ilow])*2/alpha sumhigh=sum(actual[ihigh]-predObj[ihigh,3])*2/alpha avglength=sumlength/n IS=(sumlength+sumlow+sumhigh)/n # average length + average under/over penalties cover=mean(actual>= predObj[,2] & actual<=predObj[,3]) summ=c(alpha,avglength,IS,cover) summ } |
Some helper functions
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
prediction_ts <- function(model, forwardstep){ #model is the arma-grach model fitted #ts is the historical ts #forwardstep is the number of steps to predict forecast = ugarchforecast(model, n.ahead = forwardstep) return(forecast) }#return forcasted s4 object #notice in this case the ts should be a adjuctive ts of the seris used to fit the model determin_trian_test_size <- function(id){ recod_by_id = num_rec_by_id[num_rec_by_id$bond_id == id,]$n ntrain = round(0.6*recod_by_id) ntest = recod_by_id - ntrain size = c(ntrain,ntest) return(size) } #return c(ntrain,ntest) #test: determin_trian_test_size(9563) WORKS split_ts <- function(tsdata,ntest){ ntrain = length(tsdata) - ntest ts_train = tsdata[1:ntrain] ts_test = tsdata[(ntrain+1):length(tsdata)] return(list(ts_train,ts_test)) }#return list(train_ts,test_ts) y values |
Then the model with no external regressor is
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
model_fitting <- function(hyper,train){ #hyper is a 4 dimentional vector (p1,q1,p2,q2) #train is a ts/vector used for training spec <- ugarchspec(variance.model = list(model = "sGARCH", garchOrder = hyper[3:4], submodel = NULL, external.regressors = NULL, variance.targeting = TRUE), mean.model = list(armaOrder = hyper[1:2], external.regressors = NULL, distribution = "std", start.pars = list(), fixed.pars = list())) garch <- ugarchfit(spec = spec, data = train ,solver ='hybrid',solver.control = list(trace=0)) return(garch) }#return model. Solver is set tobe 'hybrid' inorder for convergence |
Then the fitting process
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
#give pq,iterate over bond_id performance <- function(hype){ listof_wesp_in = c() listof_wesp_out = c() listof_rmse_in = c() listof_rmse_out = c() dataframe_forISplus = c(1,1,1,1) for(i in 1:length(bond_ids)) { bondid = bond_ids[i] bond_subset = TS_whole_data[TS_whole_data$bond_id == bondid,] nforward = determin_trian_test_size(bond_ids[i])[2] ntrain = dim(bond_subset)[1] - nforward c = split_ts(bond_subset$curve_trade_diff,nforward) ts_test = as.numeric(unlist(c[2])) ts_train = as.numeric(unlist(c[1]) ) skip_to_next <- FALSE tryCatch(model_fitting(hype, ts_train), error = function(e) {skip_to_next <<- TRUE}) if(skip_to_next) { next } skip_to_next <- FALSE model = model_fitting(hype, ts_train)#s4 object tryCatch(prediction_ts(model,nforward), error = function(e) {skip_to_next <<- TRUE}) if(skip_to_next) { next } prediction = prediction_ts(model,nforward) #s4 object outsample_ressidual = ts_test - prediction@forecast$seriesFor #performance evaluation ##WESP wesp_in = WMSE_res(model@fit$residuals,head(bond_subset$re_weight,ntrain)) listof_wesp_in = c(listof_wesp_in, wesp_in) wesp_out = WMSE_res(outsample_ressidual,tail(bond_subset$re_weight,nforward)) listof_wesp_out = c(listof_wesp_out, wesp_out) #rmse rmse_in = MSE_res(model@fit$residuals) listof_rmse_in = c(listof_rmse_in, rmse_in) rmse_out = MSE_res(outsample_ressidual) listof_rmse_out = c(listof_rmse_out, rmse_out) #IS, coverage rate, average length dof = length(ts_test)-1 qt_.5 = -qt(0.25, df=dof) qt_.8 = -qt(0.1, df=dof) predicted_ts= as.vector(prediction@forecast$seriesFor) predicted_lb_ts_.5 = as.vector(prediction@forecast$seriesFor)-qt_.5*prediction@forecast$sigmaFor predicted_up_ts_.5 = as.vector(prediction@forecast$seriesFor)+qt_.5*prediction@forecast$sigmaFor predicted_lb_ts_.8 = as.vector(prediction@forecast$seriesFor)-qt_.8*prediction@forecast$sigmaFor predicted_up_ts_.8 = as.vector(prediction@forecast$seriesFor)+qt_.8*prediction@forecast$sigmaFor predobject_.5 = cbind(predicted_ts,predicted_lb_ts_.5,predicted_up_ts_.5) predobject_.8 = cbind(predicted_ts,predicted_lb_ts_.8,predicted_up_ts_.8) a = intervalScorePlus(predobject_.5,ts_test,0.5) b = intervalScorePlus(predobject_.8,ts_test,0.8) dataframe_forISplus <- rbind(dataframe_forISplus,a,b) } dataframe_forISplus <- dataframe_forISplus[-1,] dataframe_forISplus <- as.data.frame(dataframe_forISplus) colnames(dataframe_forISplus) <- c("alpha", "Averagelength", "IS", "Coverage_Rate") rownames(dataframe_forISplus) <- 1:dim(dataframe_forISplus)[1] mean_.5_avelength = mean(dataframe_forISplus$Averagelength[dataframe_forISplus$alpha == 0.5]) mean_.8_avelength = mean(dataframe_forISplus$Averagelength[dataframe_forISplus$alpha == 0.8]) mean_.5_IS = mean(dataframe_forISplus$IS[dataframe_forISplus$alpha == 0.5]) mean_.8_IS = mean(dataframe_forISplus$IS[dataframe_forISplus$alpha == 0.8]) mean_.5_covrate = mean(dataframe_forISplus$Coverage_Rate[dataframe_forISplus$alpha == 0.5]) mean_.8_covrate = mean(dataframe_forISplus$Coverage_Rate[dataframe_forISplus$alpha == 0.8]) summ = c(mean_.5_avelength,mean_.8_avelength,mean_.5_IS,mean_.8_IS,mean_.5_covrate,mean_.8_covrate) namm = c("AverageLength_0.5","AverageLength_0.8","IS_0.5","IS_0.8","CoverageRate_0.5","CoverageRate_0.8") framm = as.data.frame(rbind(namm,summ)) colnames(framm) <- framm[1,] framm <- framm[-1,] mean_wesp_in = mean(listof_wesp_in) mean_wesp_out = mean(listof_wesp_out) mean_rmse_in = mean(listof_rmse_in) mean_rmse_out = mean(listof_rmse_out) name = c("mean_wesp_in","mean_wesp_out","mean_rmse_in","mean_rmse_out") values = c(mean_wesp_in,mean_wesp_out,mean_rmse_in,mean_rmse_out) frame = as.data.frame(rbind(name,values), header = F) colnames(frame) <- frame[1,] frame <- frame[-1,] whole_frame <- cbind(frame,framm) return(whole_frame) } |
The performance evaluation function
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
performance <- function(hype){ listof_wesp_in = c() listof_wesp_out = c() listof_rmse_in = c() listof_rmse_out = c() dataframe_forISplus = c(1,1,1,1) for(i in 1:length(bond_ids)) { bondid = bond_ids[i] bond_subset = TS_whole_data[TS_whole_data$bond_id == bondid,] nforward = determin_trian_test_size(bond_ids[i])[2] ntrain = dim(bond_subset)[1] - nforward c = split_ts(bond_subset$curve_trade_diff,nforward) ts_test = as.numeric(unlist(c[2])) ts_train = as.numeric(unlist(c[1]) ) skip_to_next <- FALSE tryCatch(model_fitting(hype, ts_train), error = function(e) {skip_to_next <<- TRUE}) if(skip_to_next) { next } skip_to_next <- FALSE model = model_fitting(hype, ts_train)#s4 object tryCatch(prediction_ts(model,nforward), error = function(e) {skip_to_next <<- TRUE}) if(skip_to_next) { next } prediction = prediction_ts(model,nforward) #s4 object outsample_ressidual = ts_test - prediction@forecast$seriesFor #performance evaluation ##WESP wesp_in = WMSE_res(model@fit$residuals,head(bond_subset$re_weight,ntrain)) listof_wesp_in = c(listof_wesp_in, wesp_in) wesp_out = WMSE_res(outsample_ressidual,tail(bond_subset$re_weight,nforward)) listof_wesp_out = c(listof_wesp_out, wesp_out) #rmse rmse_in = MSE_res(model@fit$residuals) listof_rmse_in = c(listof_rmse_in, rmse_in) rmse_out = MSE_res(outsample_ressidual) listof_rmse_out = c(listof_rmse_out, rmse_out) #IS, coverage rate, average length dof = length(ts_test)-1 qt_.5 = -qt(0.25, df=dof) qt_.8 = -qt(0.1, df=dof) predicted_ts= as.vector(prediction@forecast$seriesFor) predicted_lb_ts_.5 = as.vector(prediction@forecast$seriesFor)-qt_.5*prediction@forecast$sigmaFor predicted_up_ts_.5 = as.vector(prediction@forecast$seriesFor)+qt_.5*prediction@forecast$sigmaFor predicted_lb_ts_.8 = as.vector(prediction@forecast$seriesFor)-qt_.8*prediction@forecast$sigmaFor predicted_up_ts_.8 = as.vector(prediction@forecast$seriesFor)+qt_.8*prediction@forecast$sigmaFor predobject_.5 = cbind(predicted_ts,predicted_lb_ts_.5,predicted_up_ts_.5) predobject_.8 = cbind(predicted_ts,predicted_lb_ts_.8,predicted_up_ts_.8) a = intervalScorePlus(predobject_.5,ts_test,0.5) b = intervalScorePlus(predobject_.8,ts_test,0.8) dataframe_forISplus <- rbind(dataframe_forISplus,a,b) } dataframe_forISplus <- dataframe_forISplus[-1,] dataframe_forISplus <- as.data.frame(dataframe_forISplus) colnames(dataframe_forISplus) <- c("alpha", "Averagelength", "IS", "Coverage_Rate") rownames(dataframe_forISplus) <- 1:dim(dataframe_forISplus)[1] mean_.5_avelength = mean(dataframe_forISplus$Averagelength[dataframe_forISplus$alpha == 0.5]) mean_.8_avelength = mean(dataframe_forISplus$Averagelength[dataframe_forISplus$alpha == 0.8]) mean_.5_IS = mean(dataframe_forISplus$IS[dataframe_forISplus$alpha == 0.5]) mean_.8_IS = mean(dataframe_forISplus$IS[dataframe_forISplus$alpha == 0.8]) mean_.5_covrate = mean(dataframe_forISplus$Coverage_Rate[dataframe_forISplus$alpha == 0.5]) mean_.8_covrate = mean(dataframe_forISplus$Coverage_Rate[dataframe_forISplus$alpha == 0.8]) summ = c(mean_.5_avelength,mean_.8_avelength,mean_.5_IS,mean_.8_IS,mean_.5_covrate,mean_.8_covrate) namm = c("AverageLength_0.5","AverageLength_0.8","IS_0.5","IS_0.8","CoverageRate_0.5","CoverageRate_0.8") framm = as.data.frame(rbind(namm,summ)) colnames(framm) <- framm[1,] framm <- framm[-1,] mean_wesp_in = mean(listof_wesp_in) mean_wesp_out = mean(listof_wesp_out) mean_rmse_in = mean(listof_rmse_in) mean_rmse_out = mean(listof_rmse_out) name = c("mean_wesp_in","mean_wesp_out","mean_rmse_in","mean_rmse_out") values = c(mean_wesp_in,mean_wesp_out,mean_rmse_in,mean_rmse_out) frame = as.data.frame(rbind(name,values), header = F) colnames(frame) <- frame[1,] frame <- frame[-1,] whole_frame <- cbind(frame,framm) return(whole_frame) } |
Result


The performance distribution of different combinations is

The scale of the graph above shows that all combinations of p and q have a super similar performance. The best model is ARMA(3,1)−GARCH(1,0)with trade size as an external regressor.
Summary
This is quite an interesting experience. Afterward, as I do some own research, this is a very popular model used in financial modeling. The method applied here can be approved better. It can be more precise if the treasury bond interest rate were merged into the data set and do the curve price computation by ourselves instead of using the given curve-based price.
The project is much longer than what I showed above. It starts with data cleaning and necessary PCA and transformation. I just showed the part I did. I attached my code and data set here in case of your interest.
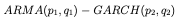
Leave a Reply